Segmentation, Mapping, Text

UCSD MGT 100 Week 02

Kenneth C. Wilbur and Dan Yavorsky

Segmentation

Putting the S into STP
Note: I don’t duplicate the reading

Heterogeneity

A fancy way to say that customers differ, e.g.

Product needs–usage intensity, frequency, context; loyalty

- Most important dimension of heterogeneity, by far
- This perspective differs from the reading

Demographics–often overrated as predictors of behavior
Psychographics–Orientation to Art, Status, Religion, Family, …
Location
Experience
Information
Attitudes
Differences may predict purchases, wtp, usage, satisfaction, retention, …

Market Segmentation

Segments: distinct customer groups with similar attributes within a segment, different attributes between segments

    - Fundamental since the 1960s
    - Numerous segmentation techniques exist
    - Customer Response Profiles embody segments
    - B2B segments: customer needs, size, profitability, internal structure

Segmentation should drive most customer decisions

Segments in this class, ranked by size

BE majors uninterested in Customers/Marketing
BE majors interested in Customers/Marketing
Non-BE majors, often minoring in Business, Marketing or Business Analytics

Measurable

Substantial

Is segmenting by gender sexist?

Customer demographics

In some markets– makeup, diapers, sports, shoes– demographics correlate strongly with behaviors
In most markets– smartphones, universities, software, cars– demographics correlate weakly with behaviors
Demographics don’t typically cause purchases, except when they predict real differences in customer needs
Why do we so often overrate demographics as predictors of behavior?

Segmentation in Action

Who does it
Browser example
Why we keep it quiet

Nearly every large business segments its markets

Firefox User Types

Firefox User Types

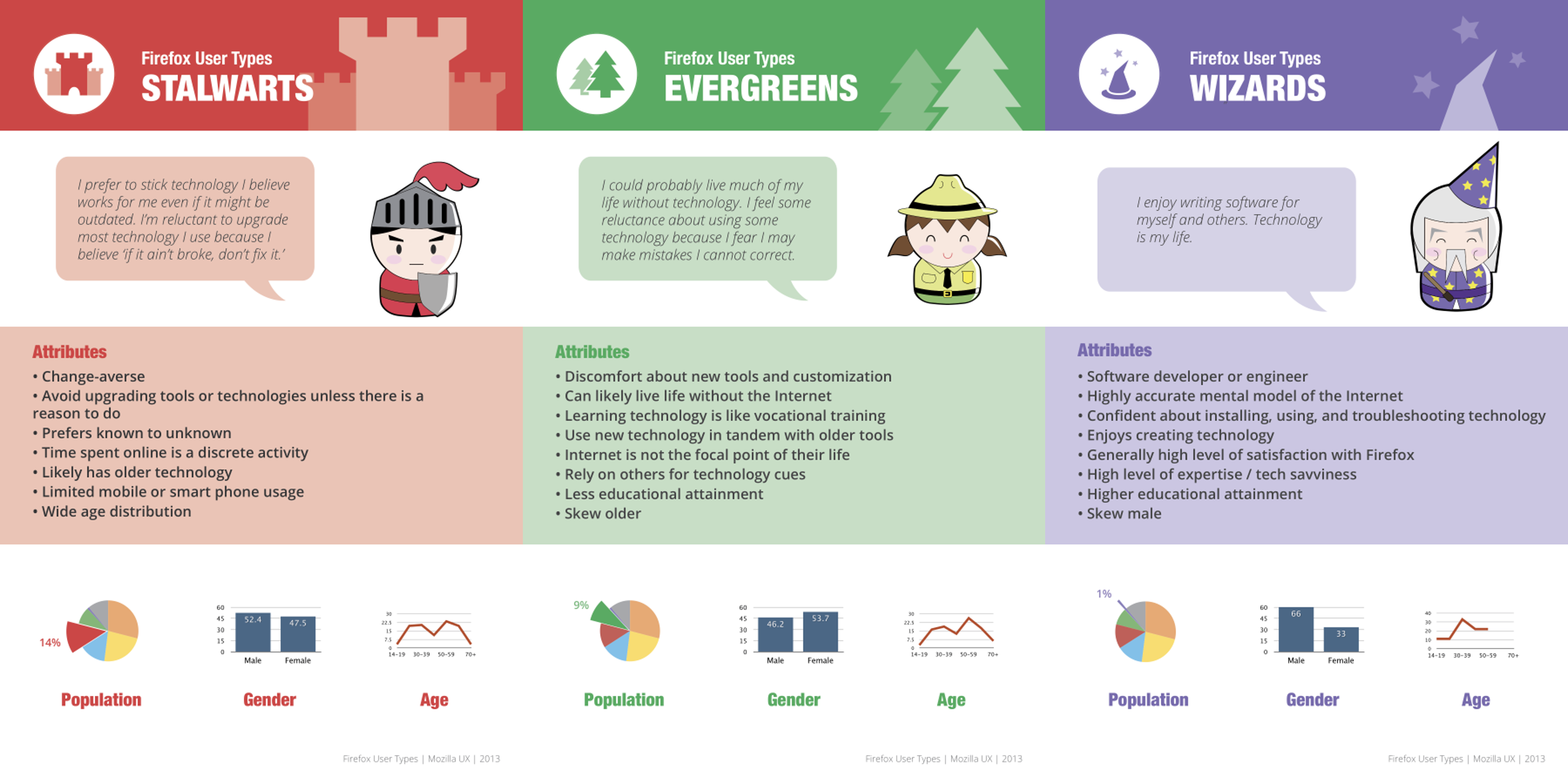
Firms don’t publicize segments

UO website: “We stock our stores with what we love, calling on our — and our customer’s — interest in contemporary art, music and fashion. …
“We offer a lifestyle-specific shopping experience for the educated, urban-minded individual in the 18 to 30 year-old range…’’

Firms don’t publicize segments

Earnings call: “Our customer is from traditional homes and advantage, but this offers them the benefit of rebellion…
Our customer is exposed to new ideas and philosophies. This can be a real involvement and work, or it could be just talk.
Irreverence and concern can live together. Often products sell well that represent the concerns they have but also can speak to their irreverence.
Our customer leads a pretty cloistered existence although they deem themselves worldly…they believe that they’re right and they believe that everything that’s happening to them is what’s happening everywhere.
Our customer is highly involved in mating and dating behavior…one of the primary drives for their spending behavior…they work hard to postpone adulthood… ’’

Firms don’t publicize segments

A. website: “a lifestyle brand that catered to creative, educated and affluent 30-45 year-old women…
“Our customer is a creative-minded woman, who wants to look like herself, not the masses. She has a sense of adventure about what she wears, and although fashion is important to her, she is too busy enjoying life to be governed by the latest trends.’’

Firms don’t publicize segments

Earnings call: “We don’t think of her in terms of age or affluence or even location. We try to think of her in her life stage and her sensibilities.
“She’s recently wed. She’s settling down. She’s very interested less in the mating rituals and actually has been trying and building and creating an environment she wants to live in for herself and family.
“She loves art and culture… And clothing and her living environment to her are canvases in which she’s able to express and control her life, whereas workplace and those things around her, she may not control.
“We believe in many ways that’s what’s touched her and connect her to Anthropologie and why she is more loyal to us than to most retailers.’’

How we segment

Customer Data Platform (CDP)
Data Marketplaces

Customer Data Platform (CDP) - 4 jobs

Data collection

  Intake data from numerous disparate sources:
  In-house, direct partners, data brokers, public data

Data unification or harmonization

  Authenticate and de-duplicate rows and columns

Data comprehension

  Generate inferences, test hypotheses, make predictions, estimate models
  Covers descriptive, diagnostic & predictive analytics

Data activation

  Prescriptive analytics: Use data to inform and automate marketing actions

Data Marketplaces

Automated platforms for transacting & transmitting data e.g. AWS Data Exchange, Databricks Marketplace, Snowflake Marketplace
```
  Relatively recent phenomenon
```

Upsides

  Many data types and sources
  Easy subscriptions, automatic updates, automated wrangling
  Competitive marketplace may lower prices
  Enable complementarities with cloud storage, etc

Some caveats

  Low barriers to entry
  Questionable validation, trustworthiness, purchaser control
  May lead to a lemons/peaches market, but reviews may help

Suppose we segment the smartphone market according to each customer’s desired brand.
Is this a good approach?

How to pick attributes?

We want to segment based on attributes that drive sales, profit, retention. But how?

Theory, experience
Market research
Customer database
Consult customer experts (salespeople)
Find out what other firms are doing
Let sales data pick for us (het. logit)

How GBK segments

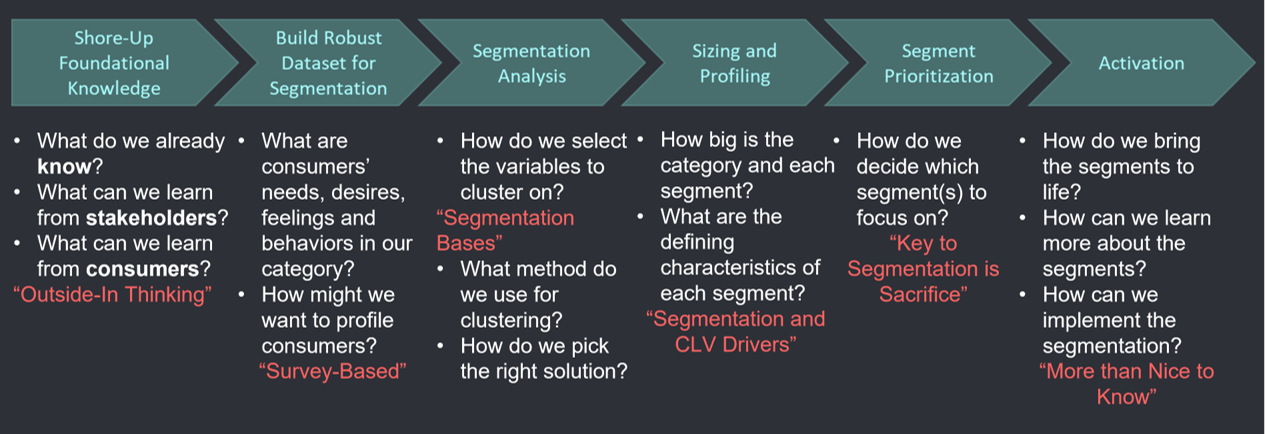
Cluster analysis

“Unsupervised learning”:
techniques to classify, describe, summarize unlabeled data

K-Means

Simple, elegant approach to define \(k=1,\ldots,K\) segments
Main idea: Choose \(K\) centroids \(\{C_1, ..., C_K\}\) to minimize total within-segment variation:

\[ \min \sum_{k=1}^K W(C_k)\]

where \(W(C_k)\) measures variation among customers assigned to segment \(k\)

K-Means

Most common \(W(C_k)\) function is Euclidean distance
Given a set of \(i \in I_k\) customers in segment \(k\), each with \(p=1,...,P\) measured attributes \(x_{ip}\),

\[ W(C_k)=\sqrt {\sum_{i \in I_k} \sum_{p} (x_{ip}-\bar{x}_{kp})^2}\]

where \(\bar{x}_{kp}\) is the average of \(\bar{x}_{ip}\) for all \(i \in I_k\), and the centroid is \(C_k=(\bar{x}_{k1}, ..., \bar{x}_{kP})\)

K-Means Algorithm

How do we assign customers to segments?
There are nearly \(K^n\) ways to partition \(n\) obs into \(K\) clusters
Happily, a simple algorithm finds a local optimum:

Randomly choose \(K\) centroids
Assign every customer to nearest centroid
Compute new centroids based on customer assignments
Iterate 2-3 until convergence

(Optional) Repeat 1-4 for many random centroids

You will run this in Week 2 script
Let's illustrate it in class

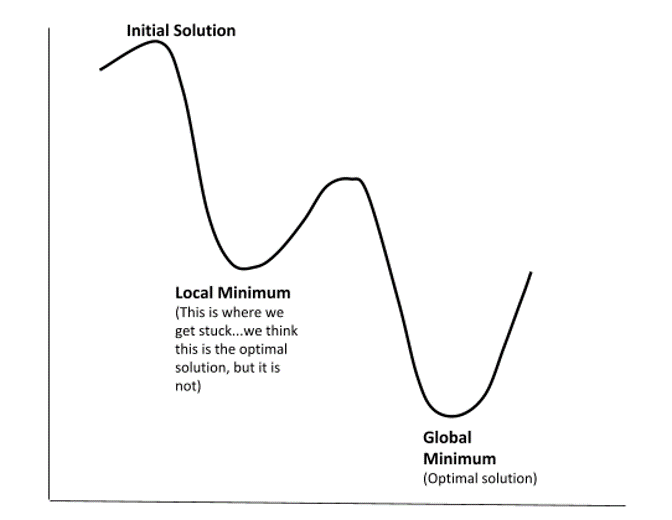
    - We usually use 'hillclimbers' to optimize numeric functions
    - Imagine I asked you to find the highest point on campus; how? On Earth?
    - W(C_k) is not globally concave, so we can't guarantee a global minimum
    - Thus, we pick many starting points, and see which offers the lowest W(C_k)
    - Note: Some algos promise to find global minimum, but this is only provable for a globally convex function. This claim can be a 'tell'

Meet your study group. Create a group chat. Schedule to meet weekly in person to discuss homework.

Market Mapping

Positioning in attribute space
Economic theories of differentiation: Vertical, horizontal
PCA & Perceptual maps

Marketing strategy

Segmentation: How do customers differ
Targeting: Which segments do we seek to attract and serve

Positioning

    - What value proposition do we present
    - How do our product's objective attributes compare to competitors
    - Where do customers perceive us to be
    - How do we want to influence consumer perceptions

Market mapping helps with Positioning

Market Maps

Market maps use customer data to depict competitive situations. Why?

  - Understand brand/product positions in the market
  - Track changes
  - Identify new products or features to develop
  - Understand competitor imitation/differentiation decisions
  - Evaluate results of recent tactics
  - Cross-selling, advertising, identifying complements or substitutes, bundles...

Market maps

We often lack ground truth data

    - Using a single map to set strategy is risky

Repeated mapping builds confidence
(“Movies, not pictures”)
Many large brands do this regularly

Vertical Diff., AKA quality

Product attributes where more is better, all else constant
- Efficacy, e.g. CPU speed or horsepower
- Efficiency, e.g. power consumption
- Input good quality (e.g. clothes, food)
Important: not everyone buys the better option (why not?)

Horizontal Diff., AKA fit or match

Product attributes w heterogeneous valuations
- Physical location
- Familiarity, e.g. what you grew up with
- Taste, e.g. sweetness or umami
- Brand image, e.g. Tide, Jif, Coca-Cola
- Complements, e.g. headphones or charging cables

Hotelling (1929)

Ice cream vendors

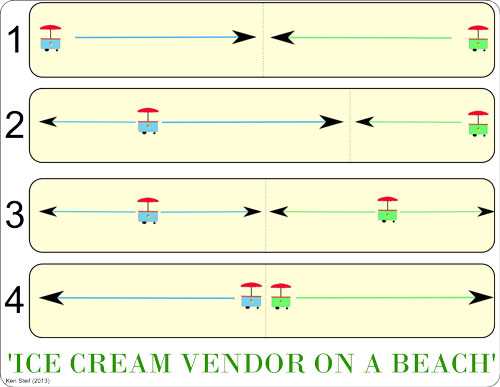
Median voter theorem

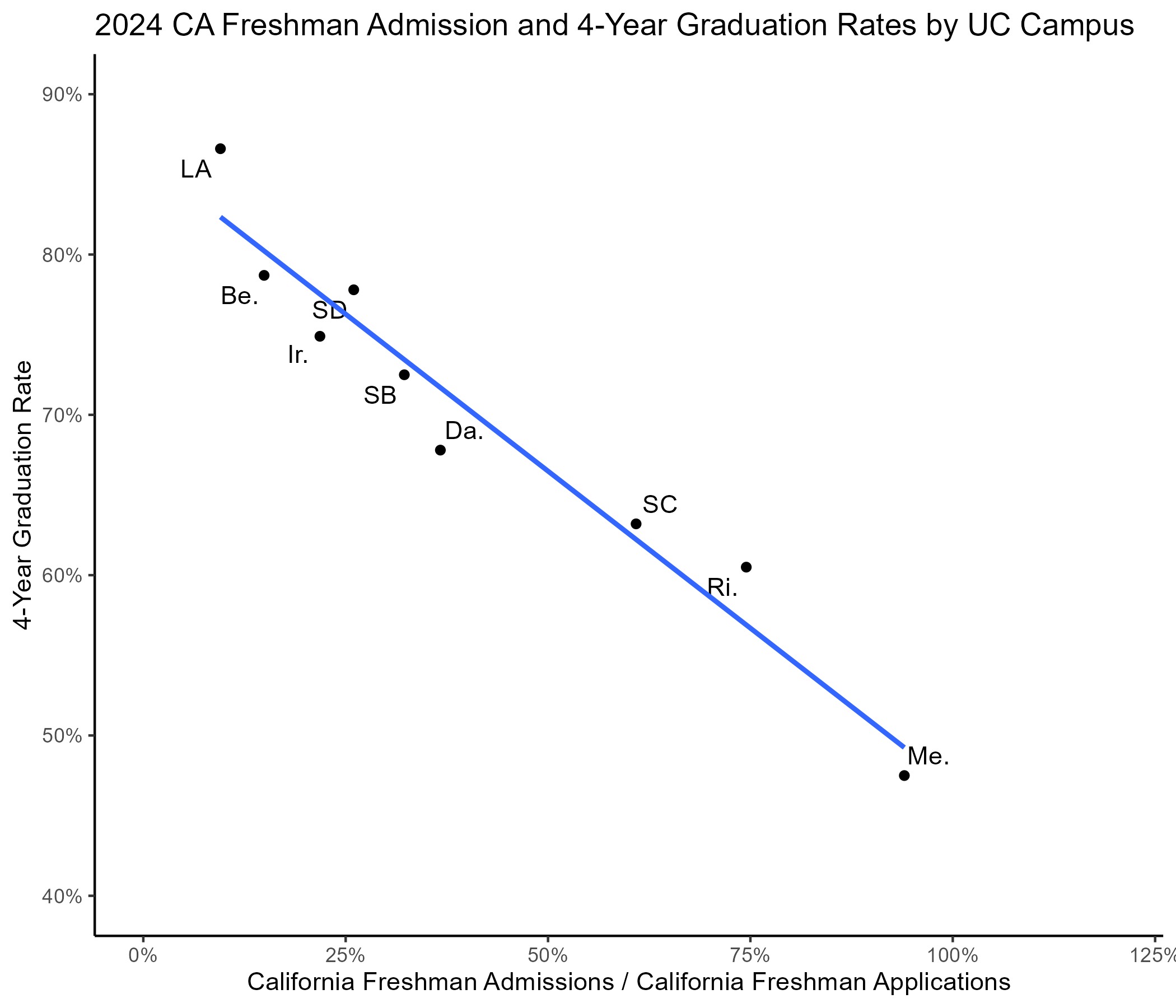
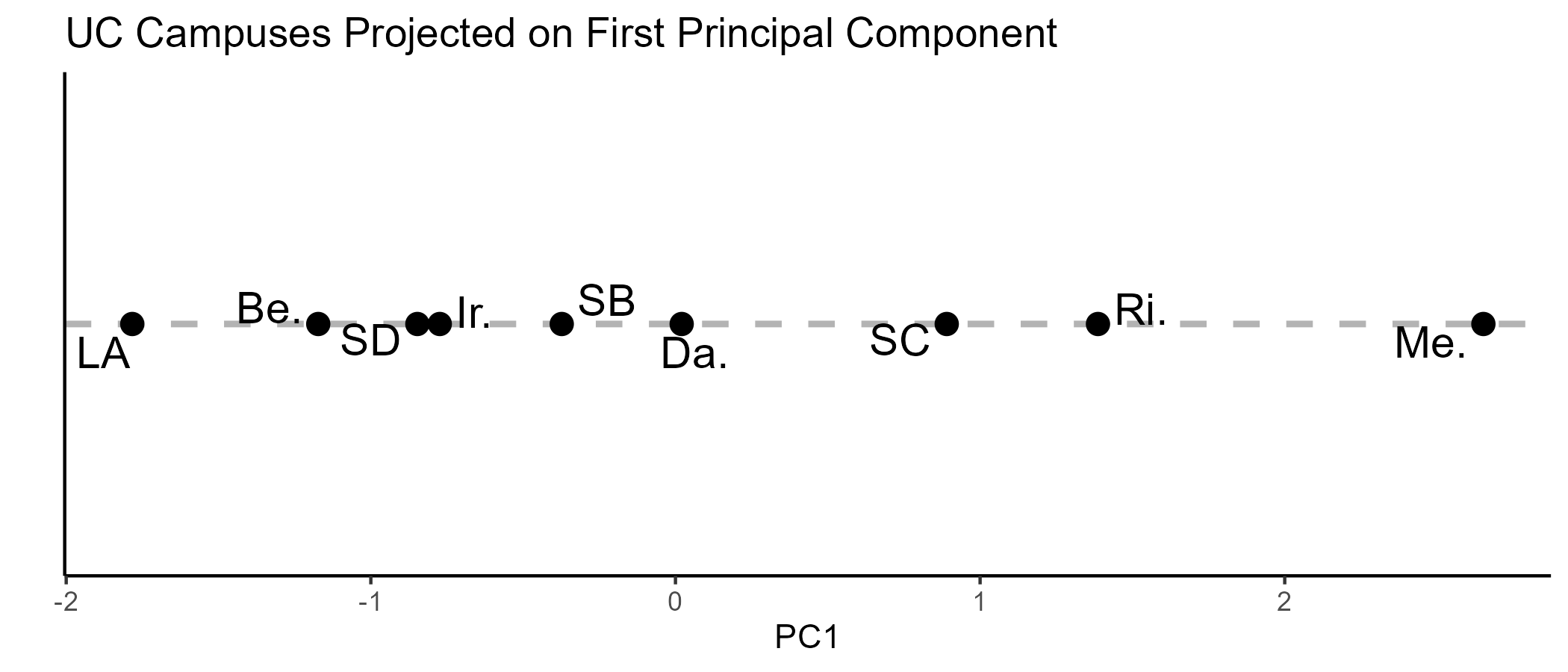
Suppose you are the UCSD Chancellor, tasked with increasing in-state freshman enrollments
You want to map UC campuses in the market for California freshman applicants

You posit that selectivity and time-to-degree matter most

    - Students want to connect with smart students
    - Students want to graduate on time

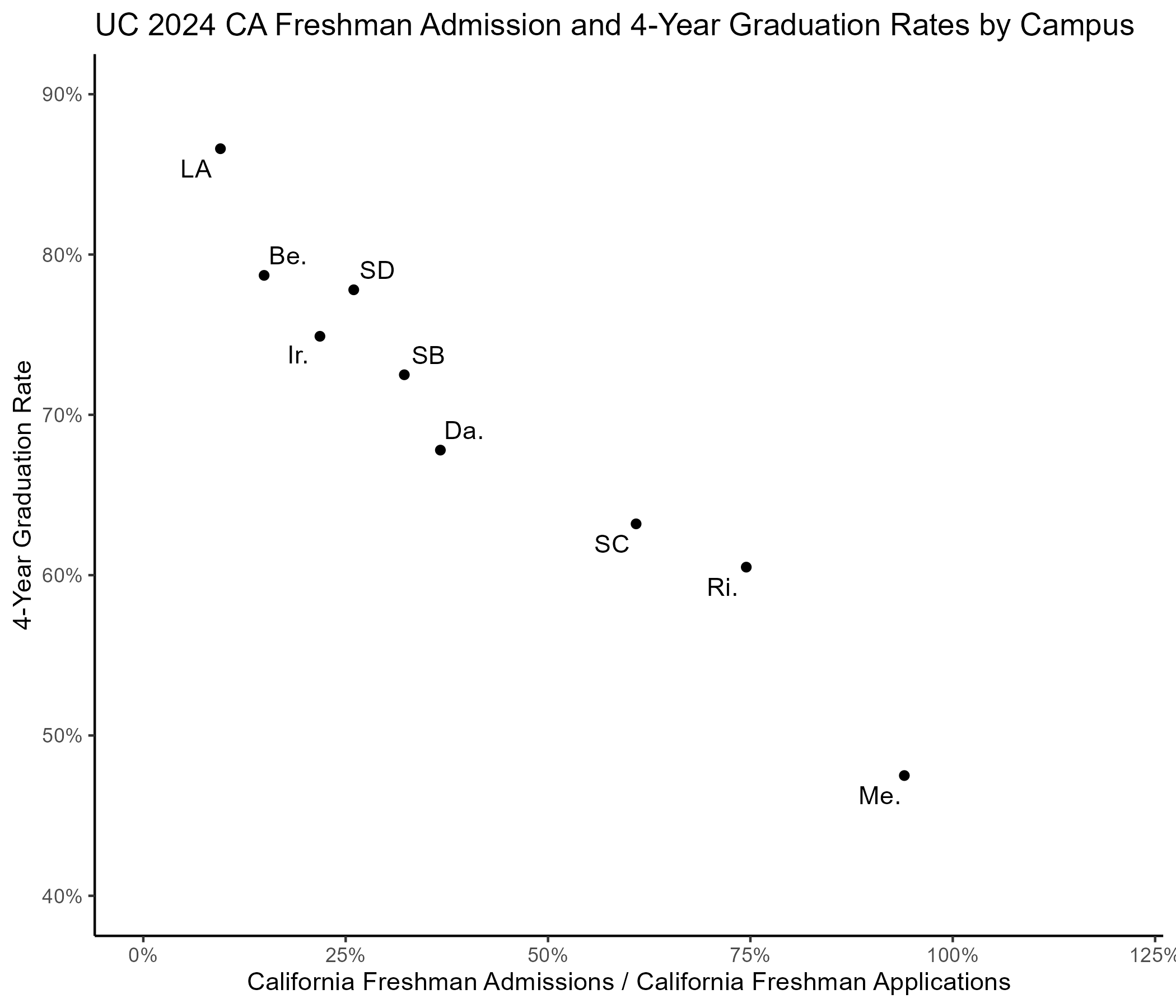
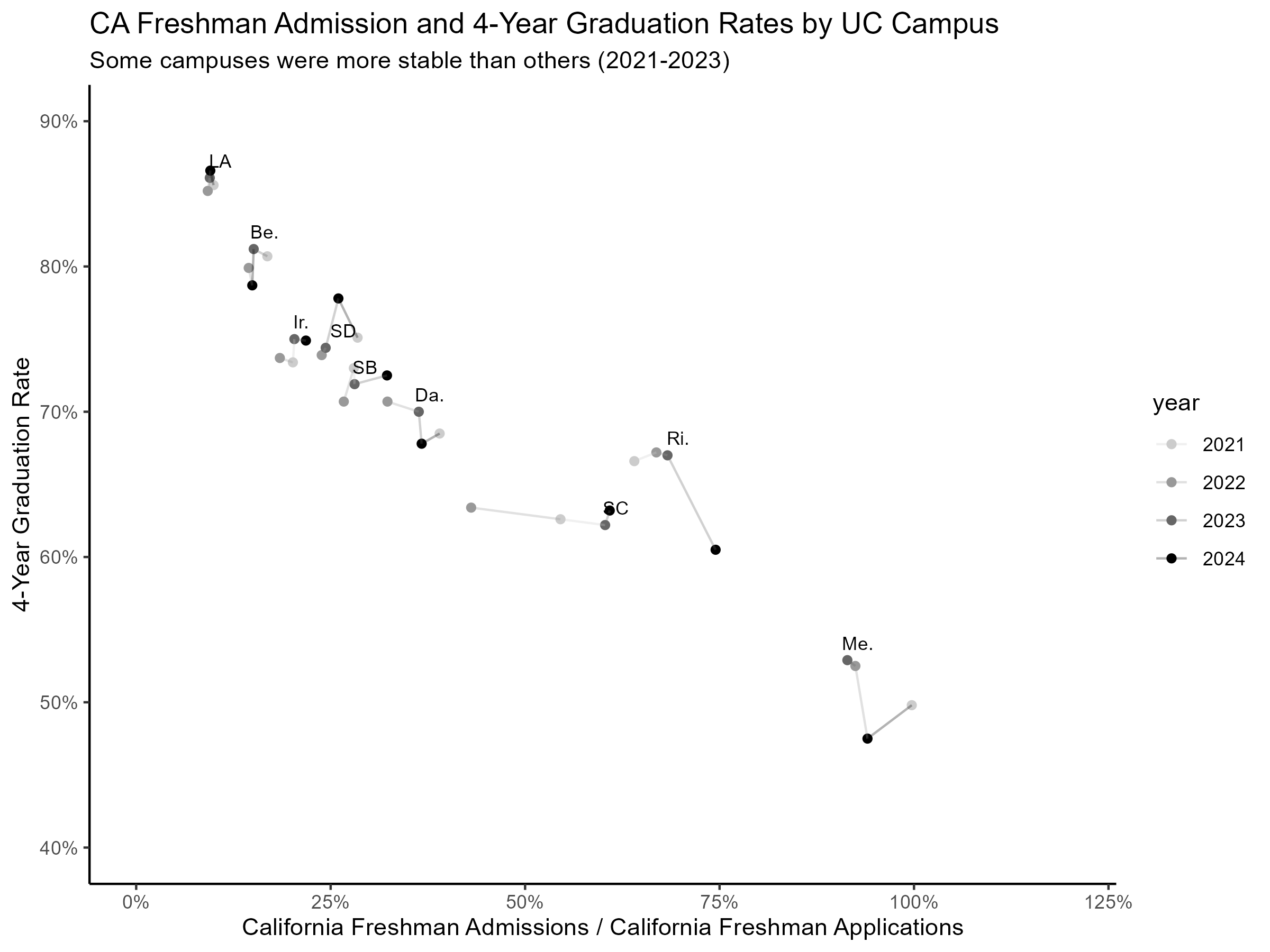
What if there are too many product attributes to graph?

Enter Principal Components Analysis

    - Powerful way to summarize data 
    - Projects high-dimensional data into a lower dimensional space 
    - Designed to minimize information loss during compression
    - Pearson (1901) invented; Hotelling rediscovered (1933 & 36)

Principal Components Analysis (PCA)

Store \(K\) continuous attributes for \(J>K\) products in \(X\), a \(J\times K\) matrix
Consider \(X\) a \(K\)-dimensional space containing \(J\) points
Calculate \(X'X\), a \(K \times K\) covariance matrix of the attributes
1st \(n\) eigenvectors of the attribute covariance matrix give unit vectors to map products in \(n\)-dimensional space
```
   - We'll use first 1 or 2 eigenvectors for visualization
```

PCA FAQ

How do I interpret the principal components?

   - Each principal component is a linear combination of the larger space's axes
   - Principal components are the "new axes" for the newly-compressed space
   - Principal components are always orthogonal to each other, by construction

What are the main assumptions of PCA?

   - Variables are continuous and linearly related
   - Principal components that explain the most variation matter most
   - Drawbacks: information loss, reduced spatial interpretability, outlier sensitivity

How do I choose the # of principal components?

   - Business criteria: 1 or 2 if you want to visualize the data
   - Business criteria: Or, value of compressed data in subsequent operations 
   - Statistical criteria: Cume variance explained, scree plot, eigenvalue > 1

What are some similar tools to PCA?

   - Factor analysis, linear discriminant analysis, independent component analysis...

How does PCA relate to K-means?

K-Means identifies clusters within a dataset

    - K-Means augments a dataset by identifying similarities within it
    - K-Means never discards data

PCA combines data dimensions to condense data with minimal information loss

    - PCA is designed to optimally reduce data dimensionality
    - PCA facilitates visual interpretation but does not identify similarities

Both are unsupervised ML algos

   - Both have "tuning parameters" (e.g. # segments, # principal components)
   - They serve different purposes & can be used together
   - E.g. run PCA to first compress large data, then K-Means to group points
   - Or, K-Means to identify clusters, then PCA to visualize them in 2D space

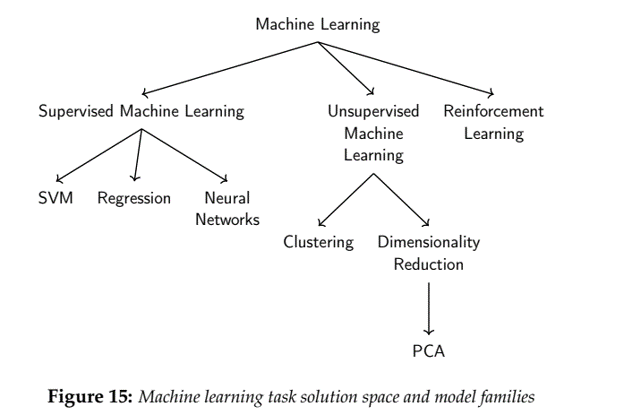
Conceptual organization

Mapping Practicalities

How to measure intangible attributes like trust?

   - Ask consumers, e.g. "How much do you trust this brand?"
   - Marketing Research techniques measure subjective attributes and perceptions

What if we don’t know, or can’t measure, the most important attributes?
```
   - Multidimensional scaling
```
How should we weigh attributes?

Do we know the most important attributes?

Multidimensional scaling draws perceptual maps

Suppose you can measure product similarity

For \(J\) products, populate the \(J\times J\) matrix of similarity scores

   - With J brands, we have J points in J dimensions. Each dimension j indicates similarity to brand j. PCA can projects J dimensions into 2D for plotting

Use PCA to reduce to a lower-dimensional space

   - Pro: We don't need to predefine attributes
   - Con: Axes can be hard to interpret

Multidimensional scaling

MDS Intuition, in 2D space

      - With a ruler and map, measure distances between 20 US cities ("similarity")
      - Record distances in a 20x20 matrix: PCA into 2D should recreate the map
      - But, we don't usually know the map we are recreating, so we look for ground-truth comparisons to indicate credibility and reliability

Examples:

      - Poli Sci: Political candidate positioning, eg left to right
      - Psychologists: Understand perceptions and evaluation of personality traits
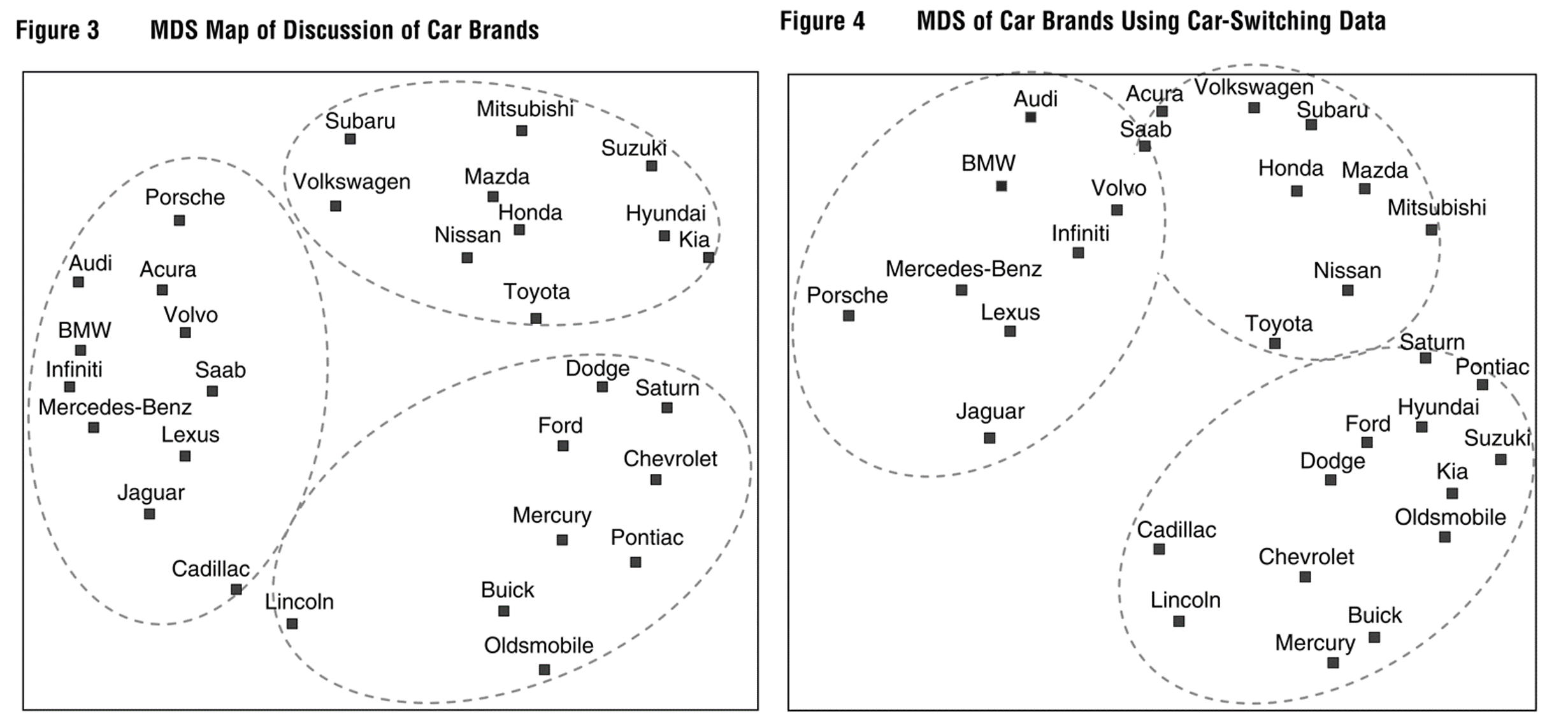
      - Marketers: how consumers perceive brands or products

Example: Netzer et al. (2012)

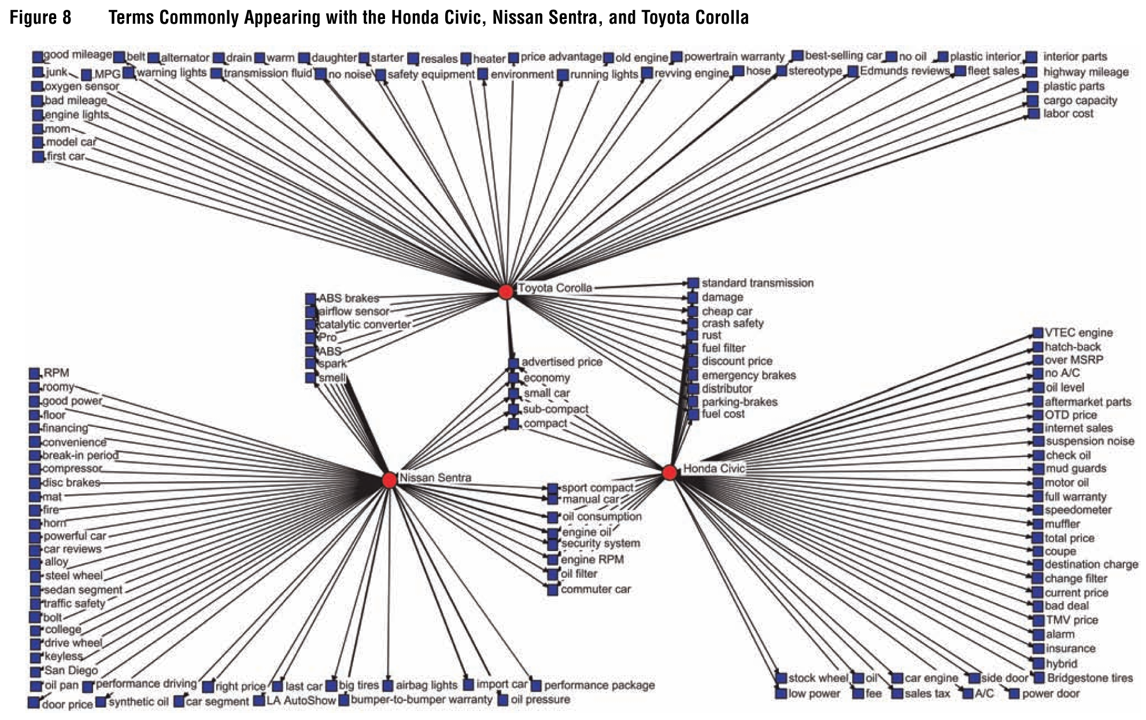
How to weigh product attributes?

Demand modeling uses product attributes and prices to explain customer purchases

Heterogeneous demand modeling uses product attributes, prices and customer attributes to explain purchases

      - "Revealed preferences": Demand models explain observed choices in uncontrolled market environments

Text data

The Challenge
Embeddings
LLMs: What are they doing
What does it all mean?

The Challenge

Suppose an English speaker knows \(n\) words, say \(n=10,000\)

How many unique strings of \(N\) words can they generate?

    - N=1: 10,000
    - N=2: 10,000^2=100,000,000
    - N=3: 10,000^3=1,000,000,000,000=1 Trillion
    - N=4: 10,000^4=10^16
    - N=5: 10,000^5=10^20
    - N=6: 10,000^5=10^24=1 Trillion Trillions
    - ....

Why do we make kids learn proper grammar?

    - Average formal written English sentence is ~15 words

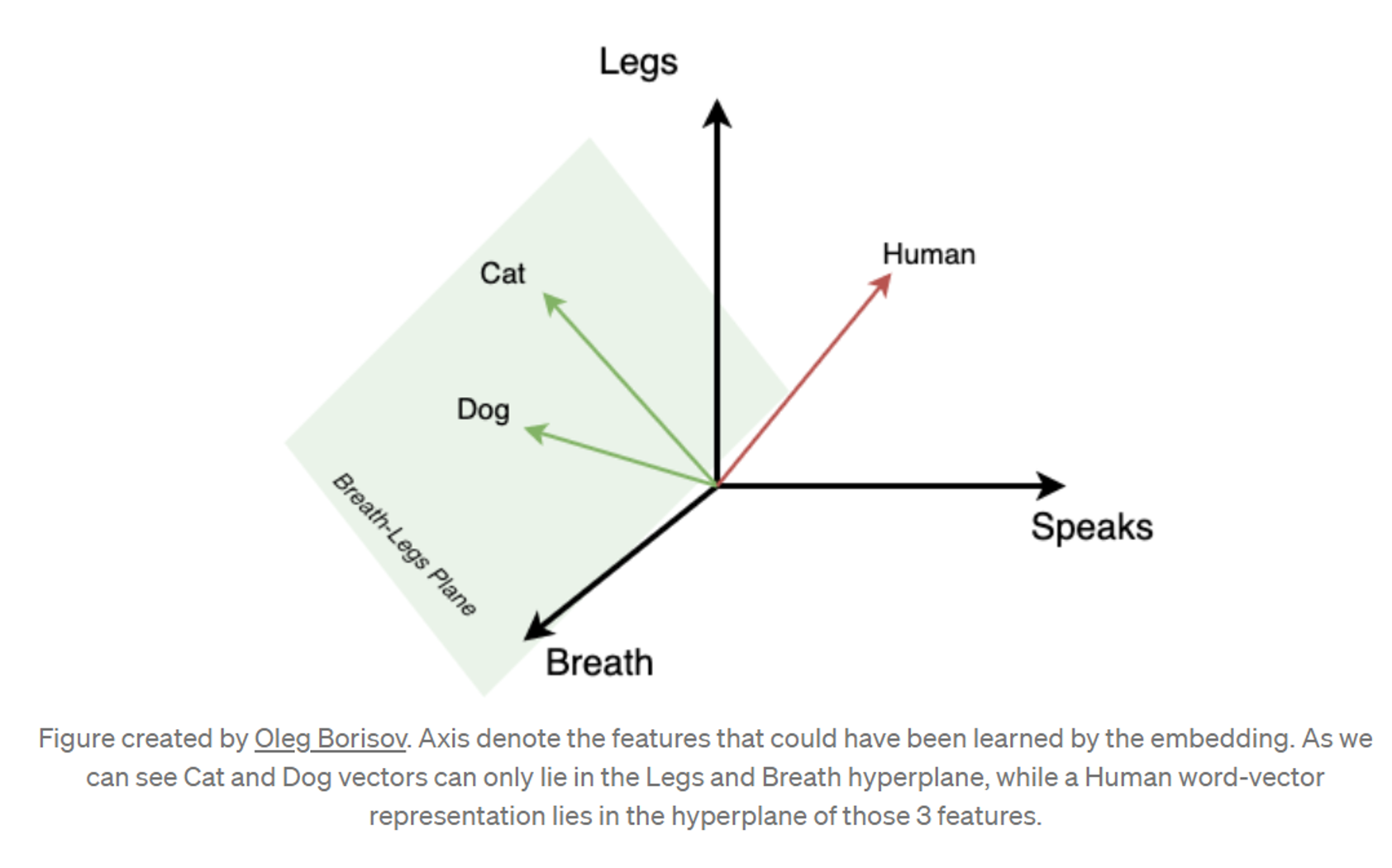
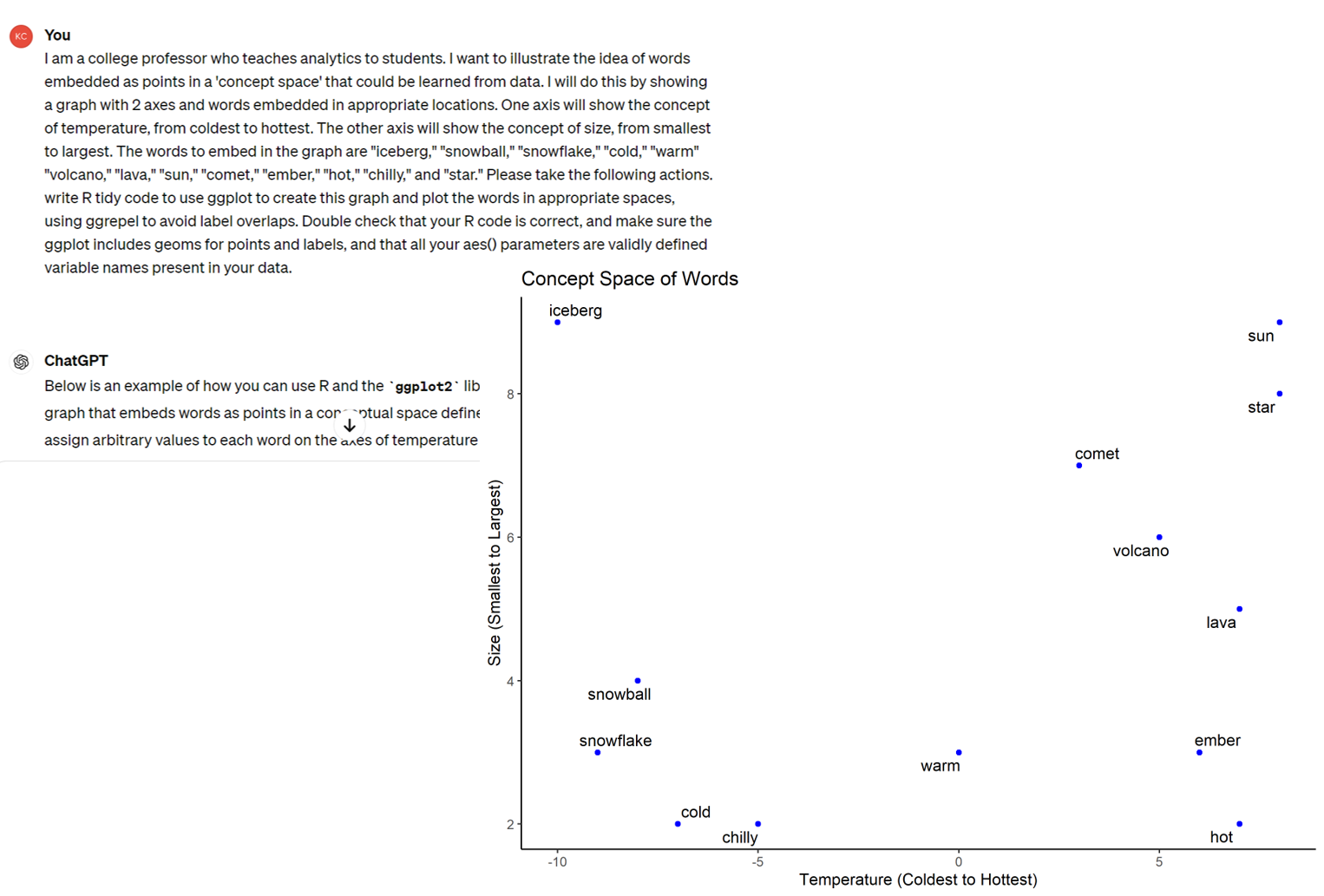
Embeddings

represent words as vectors in high-dim space

    - Really, "tokens," but assume words==tokens for simplicity

Assume \(W\) words, \(A<W\) abstract concepts

    - Assume we have all text data from all history. Each sentence is a point in $W$-dimensional space

We could run PCA to reduce from \(W\) to \(A\) dimensions

    - Assume we have infinite computing resources
    - We now have every sentence represented as a point in continuous A-space

Cool things about embeddings

Compression stores enormous textual data in a small space, other than human memory
We can do math using words!

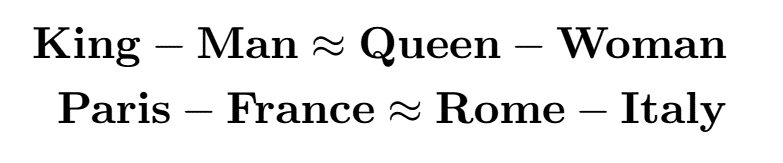
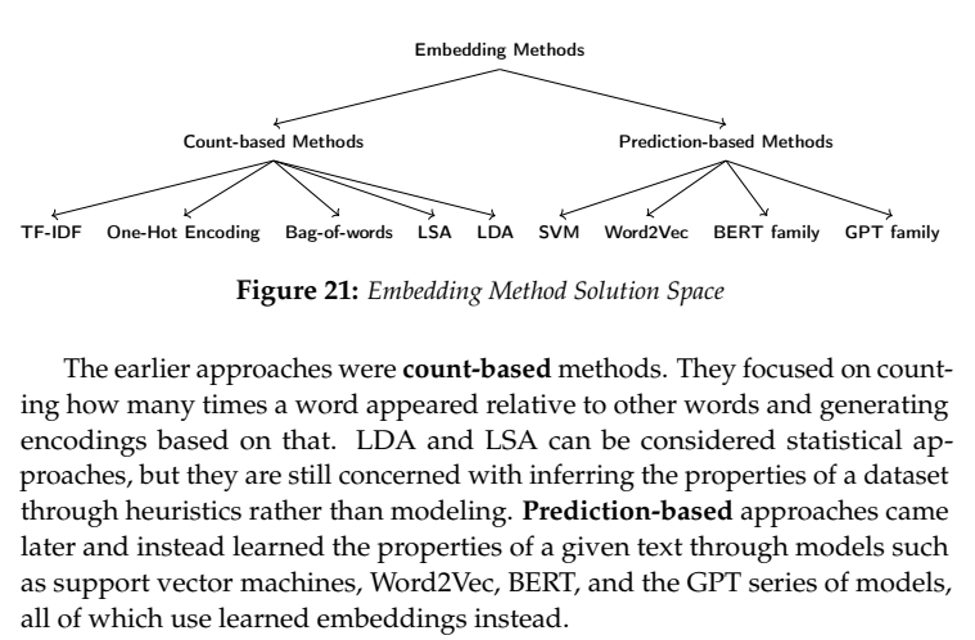
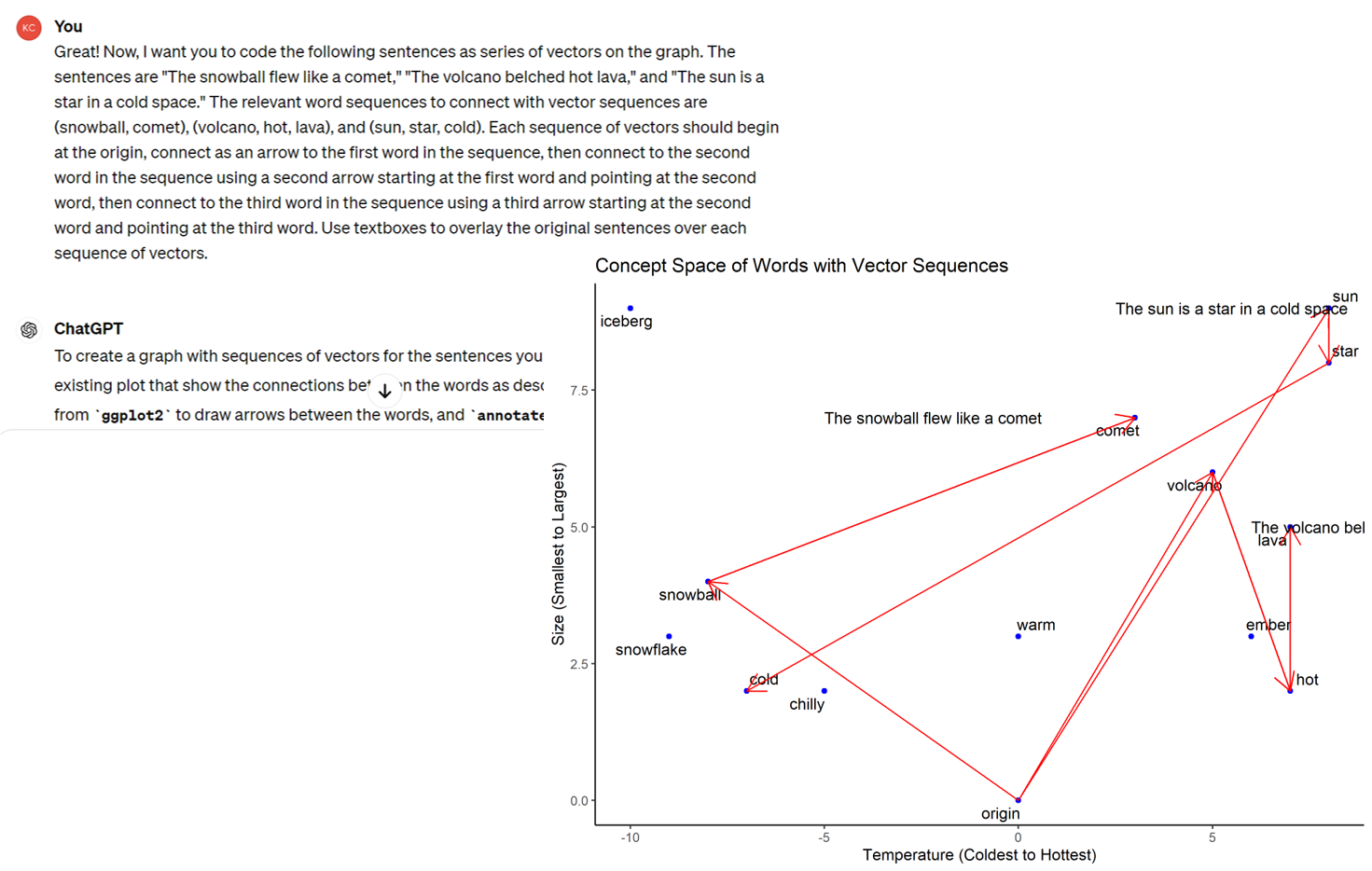
Many ways to encode embeddings

LLMs: Given a prompt,

Recode prompt to maximize contextual understanding

   - 'the bank of the river is steep' vs 'the bank near the river is solvent'
   - This is the 'attention' step you hear a lot about
   - Basically, modify every word's location based on every other word's position in the prompt sequence

Feed recoded prompt into transformer as a sequence of points in concept-space
Predict the next point and add it to the sequence
Repeat step 3 until no more good predictions
Repeat steps 1-4 many many times, then hire humans to evaluate results, use evaluations for RLHF to refine the process
Add ‘reasoning’ via reinforcement learners, and ‘deep research’ via agentic tool use
Sell access to customers, then train a bigger LLM

Example: Concept Space

Example: Sentences as Vector Sequences

What LLMs Can and Can’t Do

Can generate intelligible semantic sequences
Can summarize large text training data sets
Can help humans save time and effort in semantic tasks
Can uncover previously unknown relations in training data

Can’t distinguish truth from frequency in training data

    - LLMs propagate popular biases in training data, unless taught otherwise

Can’t reliably evaluate sequences absent from training data
Can’t discover new relationships absent in training data

Can’t think, reason, imagine, feel, want, question

    - But might complement other components that do such things

What happens next?

No way to know. The tech is far ahead of science

    - LLMs are productive combinations of pre-existing components
    - This is normal: Eng/ML/stats theory chases applications 
    - Spellchecker and calculator are not productive analogies

My guesses

    - "It's easy to predict everything, except for the future."
    - Simple tasks: LLMs outcompete humans 
    - Medium-complexity tasks: LLMs help low-skill humans compete 
    - Complex tasks: Skillful LLM use requires highly skilled humans
    - Law matters a LOT: Liability, copyright, privacy, disclosure
    - In eqm, typical quality should rise; *not* using LLMs will handicap
    - Long term: More automation, more products, more concentration of capital 
    - More word math techniques will be invented, some will be useful

What future tech might complement LLMs?

    - Reframes current argument about Sentient AI 
    - Robots? World models? Causal reasoning engines? Volition?

Class script

Standardizing variables
Iris example
Running & graphing kmeans
Use PCA to map the smartphone market

Wrapping up

Recap

Segmentation should be based on customer needs
Customer behavior best predicts behavior (not demos)
Market maps depict competition, aide positioning
PCA projects high-dim data into low-dim space w minimal information loss
Embeddings represent words as points in concept-space, enabling word-math
```
  Next week's reading helps avoid or reduce struggle
```

Going further