Demand Modeling
UCSD MGT 100 Week 3
Demand Curves
- Theory
- Challenges
- What firms do
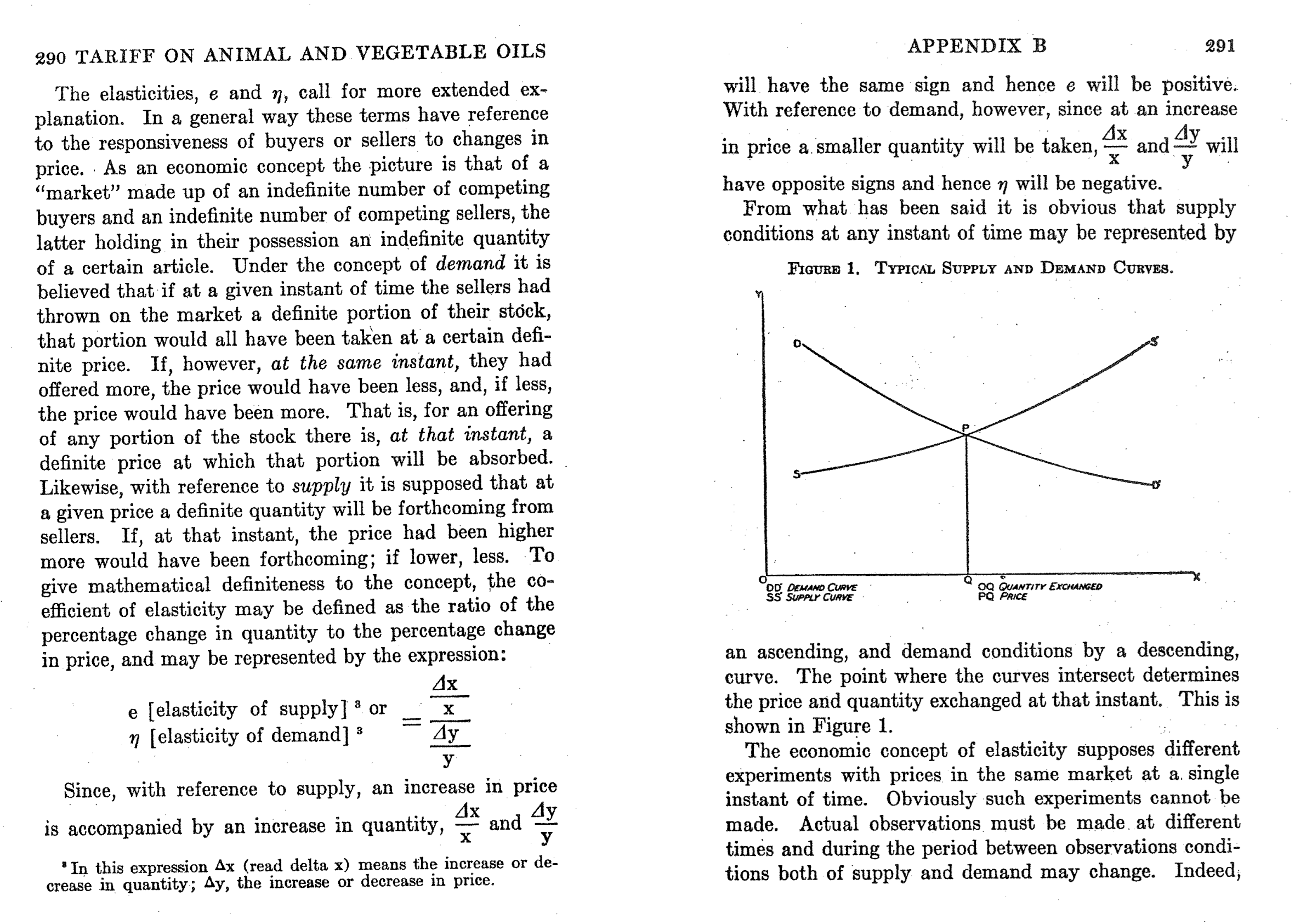
Inverse Demand Curve
Demand Curves: Theory
Useful theoretical concept that summarizes market response to price
- Why is it useful?Often taught with perfect competition
- Typically assumes stable, competitive, frictionless markets w free entry, full information, no differentiation - Model predicts zero LR economic profits - Any evidence?Also, taught with monopoly i.e. market power
- What is market power? How would we measure it?
Demand Curves: Challenges
Idealized demand curves are hard to estimate (why?)
Where do product attributes come in?
- What if we don't observe all attributes? "Price endogeneity"Many things can predict demand
- preferences, information, advertising, quality, match value, quality, complements, substitutes, competitor prices, entry, taxes and other policies, retail distribution, nature of equilibrium, stockpiling, consumer income, ...What do we need to estimate Demand?
- Observable, exogenous variation in costs or price - Otherwise, "price endogeneity" will bias demand estimates
How firms learn demand
Market research
- Conjoint analysis, customer interviews, simulated purchase environmentsExpert judgments, e.g. salesforce input
Cost-driven price adjustments
- Often one-sidedDemand modeling with archival data
Price experiments
- Market tests, digital experiments, bandits, digital couponsBest practice: triangulation
Price Experiments
Ideally, the best way to learn demand, because you create exogenous price variation; but…
Competitors & consumers can observe price variation
May change purchase timing, stockpiling or
reference pricesCompetitors, distribution partners or suppliers may react
Hence, experimenting to learn demand may change future demand
Demand Modeling: Pros
Relatively inexpensive for large organizations
Fully compatible with price experiments
- Either/or framing would be a false dichotomy: "Yes-and"Confidential, fast
Depends on real consumer choices, i.e. revealed preferences
- As opposed to stated preferencesEnables demand predictions at counterfactual prices
Enables predictions of competitor pricing response
Prediction accuracy: evaluable after price changes
Demand Modeling: Cons
Requires data, exogenous price variation, time, effort, training, commitment, trust, organizational buy-in
Always subject to untestable modeling assumptions
Requires the near future to resemble the recent past
- To be fair, all predictive analytic techniques require these 3
Do Demand Models Work?
Evidence is supportive, but not thick
- Informally, I know several people who maintain demand models in large orgs - Formal evidence requires researchers and firm to collaboratively (a) estimate demand, (b) act on demand estimates, (c) observe how actions affect outcomes, & (d) report the results publicly. Hard to do & incentives conflict - Demand modeling can also go badly, e.g. due to price endogeneityMisra & Nair (2011) : B2B sales & salesforce compensation
Nair et al. (2017) : Casino loyalty rewards
Pathak and Shi (2021) : School choice
Dube and Misra (2023) : ZipRecruiter ad pricing
Ko et al. (2024) : E-Commerce apparel promotions
Multinomial Logit
- history, math, properties, discussion
Multinomial Logit (MNL)
- Time tested, famous, popular demand model
- Ported to econ from stats & psych by McFadden (1974, 1978, 1981; “Logistic regression’’)
Multinomial Logit (MNL)
Let \(i\) index consumers, \(j=1,...,J\) products, and \(t\) index choice occasions
Assume each \(i\) gets indirect utility \(u_{ijt}\) from product \(j\) in market \(t\):
\[u_{ijt}=x_{jt}\beta-\alpha p_{jt}+\epsilon_{ijt}\]
- Then, assuming each \(i\) picks the \(j\) that maximizes \(u_{ijt}\), has unit demand, and that \(\epsilon_{ijt}\sim\)i.i.d.\(EV_1(0,1)\), market share is
\[Prob.\{u_{ijt}>u_{ikt}\forall{k\ne j}\}\equiv s_{jt}=\frac{e^{x_{jt}\beta-\alpha p_{jt}}}{\sum_{k=1}^J e^{x_{kt}\beta-\alpha p_{kt}}}\]
With \(N_t\) consumers, \(q_{jt}(\vec{x}; \vec{p})=N_t s_{jt}\). See Train 2009 sec 3.10 for proof
- Estimating \(\alpha\) and \(\beta\) enables us to predict every product’s quantity response to a change in any product’s attributes \(x_{jt}\) or price \(p_{jt}\)
MNL: Common factors
- Suppose \(\gamma_{t}\) indicates how popular the category is in market \(t\), so utility is \(u_{ijt}=\gamma_{t}+x_{jt}\beta-\alpha p_{jt}+\epsilon_{ijt}\). Then market share becomes
\[s_{jt}=\frac{e^{\gamma_{t}+x_{jt}\beta-\alpha p_{jt}}}{\sum_{k=1}^J e^{\gamma_{t}+x_{kt}\beta-\alpha p_{kt}}}\]
\[s_{jt}=\frac{e^{\gamma_{t}} e^{x_{jt}\beta-\alpha p_{jt}}}{e^{\gamma_{t}}\sum_{k=1}^J e^{x_{kt}\beta-\alpha p_{kt}}}\]
\[s_{jt}=\frac{e^{x_{jt}\beta-\alpha p_{jt}}}{\sum_{k=1}^J e^{x_{kt}\beta-\alpha p_{kt}}}\]
- Similar exercise applies to individual-specific intercepts \(\gamma_i\), or individual-time interactions \(\gamma_{it}\). Only differences across products affect predicted market shares
MNL: Share differences
- We set product \(j=1\) utility to \(u_{i1t}=\epsilon_{i1t}\) to normalize utility, i.e.
\[s_{1t}=\frac{1}{\sum_{k=1}^J e^{x_{kt}\beta-\alpha p_{kt}}}\]
- Hence for every \(j\ne 1\), consider an affine transformation of market shares:
\[ln(s_{jt})-ln(s_{1t})=x_{jt}\beta-\alpha p_{jt}\]
- Looks like a regression equation… we sometimes add an error \(\xi_{jt}\) to represent unobserved product attributes:
\[ln(s_{jt})-ln(s_{1t})=x_{jt}\beta-\alpha p_{jt}+\xi_{jt}\]
- We use the \((J-1)T\) differences in market shares to estimate demand parameters
MNL Estimation
Define \(y_{ijt} \equiv 1\{i \text{ chose } j \text{ in } t\}\). I.e., \(y_{ijt}=1\) iff \(i\) choose \(j\) at \(t\); otherwise \(y_{ijt}=0\).
- Maximum likelihood: Assume the probability of observation \(\{i,j,t\}\) is \(s_{jt}^{y_{ijt}}\);
then lik. is \(L(\beta )=\prod\limits_{\forall i,j,t} s_{jt}^{y_{ijt}}\); & choose parameters to maximize log lik:
\[\sum_{\forall i,j,t} y_{ijt}\ln s_{jt}\]
- Method of Moments: Choose \(\alpha\) and \(\beta\) to solve some vector of “moments,” i.e. interactions between exogenous observables \(z\) and error terms, e.g.
\[ \sum_{\forall j,t}z_{jt} (\frac{\sum_{\forall i}y_{ijt}}{N_t} - s_{jt})=0\]
- Linearize the model, choose parameters to minimize the sum of square errors
MNL Goodness-of-fit Statistics
Discrete choice models predict choice probabilities rather than choices, because utility is always unobserved; hence nonstandard fit statistics
Predicted outcomes are inherently stochastic, so limited predictive ability
- Likelihood Ratio Test: (not R-sq)
\[\rho=1-\frac{ln L(\hat\beta)}{ln L(0)}\]
As \(L(\hat\beta)\to 1\), \(ln L(\hat\beta)\to 0\), \(\rho\to 1\)
As \(ln L(\hat\beta)\to ln L(0)\), \(\rho\to 0\)
- Heuristic: 0.2-0.4 is pretty good
Hit Rate: % of individuals for whom most-probable choice was actually chosen
R-sq using prediction errors at the \(jt\) level
MNL Pros
Microfounded, i.e. behavioral predictions are consistent with a clearly specified theory of consumer choice
- Theory is utility maximization - Economists widely believe that microfounded models are more generalizable than purely statistical models*Extensible to accommodate preference heterogeneity
- We'll cover 3 types of extensions in heterogeneous demand modelingLikelihood function is globally concave in the parameters, ensuring fast and reliable estimation
- Remember our local vs. global optimum discussion?
MNL Cons
Assuming \(\epsilon_{ijt}\sim\)i.i.d.\(EV_1(0,1)\) is convenient but unrealistic
- More likely, more similar products would experience more similar demand shocks - Alternatives exist but can be computationally expensiveAnalyst selects the choice set \(j=1,...,J\), market size \(N_t\), attributes \(x_{jt}\), and price structure \(p_{jt}\).
- What's a j? What's a t? What's in x? How do we measure p? Who's in N? - "Tuning factors" or "Analyst degrees of freedom"Market share derivatives depend on market shares alone (IIA; see Train Sec. 3.6)
Price Endogeneity
- Affects all demand models, not just MNL
IIA: Deeper dive
- Famous example from McFadden (1974)
- Suppose you estimate demand for transportation with three options: {Blue Bus, Red Bus, Car}, each with 33% market share
- Now suppose you painted the red buses blue and want to predict market shares in the new choice set: {Blue Bus, Car}
- MNL will predict Blue Bus and Car shares of 50%, not 67% and 33% (why?)
IIA: Remedies
IIA is testable & usually rejected by data
Common remedies:
Extend the model to impose structure on choice set,
e.g. Nested Logit or Ordered LogitChange \(\epsilon_{ijt}\sim\)i.i.d.\(EV_1(0,1)\), e.g. Multivariate Probit with correlated errors
Change model structure so IIA property does not obtain, e.g. heterogeneous logit
Price endogeneity:
35 INSANE explanations
- #4 will SHOCK you. Like, comment, subscribe
- Covered on the exam…ask lots of questions
2. Fundamental issue
Demand model is a causal price-quantity relationship
Yet observed prices may correlate with other demand and supply determinants
Exogenous price variation req’d to distinguish correlation from causation (“identification”)- Price endogeneity is a "data problem" not a "model problem" - Can be hard to verify empirically--needed data is missing--but widely believed important - Implies wrong demand slope, biased demand predictionsSign of bias depends on unobserved correlation
- If corr(price,unobs)<0 --> estimated demand is "too flat" or too elastic - If corr(price,unobs)>0 --> "too steep" or too inelastic - Affects all demand models, not just MNL
3. E-Commerce Example
Imagine an unobserved demand shock, such as a viral Instagram post, increases Amazon product awareness and sales
Sales spike, inventory drops, automated pricing system increases price to monetize remaining inventory
What do data show? Corr(sales, price) > 0 !!
- Common enough to be unsurprising when this happens
4. An Analogy
Foot size data significantly predict reading comprehension among children!
- In fact, age causes both foot size - And age causes reading comprehension - Without age, you cannot accurately estimate the causal relationship between foot size and reading comprehension. You can only measure the correlation

- Also, crib purchases significantly predict childbirth!
5. Sports example
You have data on Lakers ticket prices and sales before and after the Luka trade
Prices and sales are both higher after the trade
Does this mean that higher price caused higher sales?

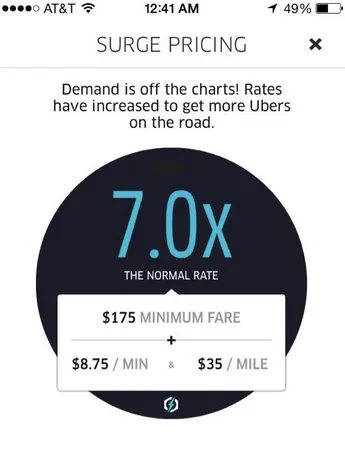
6. Example: Digital systems
Uber surge pricing:
Positive Demand shocks increase price
Negative Supply shocks increase priceSystem adjusts the price without knowing the causes
Many digital inventory-based pricing systems are similar
7. Shrinkflation

Shrink the package, maintain the price
Also, "Skimpflation" : reduce ingredient intensity8. Multiple determinants
- Price causes quantity demanded; but so do other things

9. Oft-unobserved price correlates
Changes in consumer preferences, income, market size
Retail distribution, prominence, stocking
Digital marketing, including search ads, display ads, affiliates, influencers, coupons
Competitor prices, preference shocks, retail, dig mktg
Any may correlate with equilibrium prices, leading to endogeneity biases if left uncontrolled
10. General model interpretation
Posit a model \(q=f(x,p,e)\) for \(p=\)price, \(q=\)quantity,
\(e=\)error reflecting all relevant unobservables; estimate \(\frac{dq}{dp}\)What does \(\frac{dq}{dp}\) mean exactly? 2 possibilities:
1. Correlation: Empirical tendency of q to change with p, holding other observable attributes x constant 2. Causality: Causal effect of 1-unit change of p on q 1 is descriptive analytics; 2 is diagnostic analyticsStandard econometric assumptions only admit #2 when \(corr(p,e)==0\) (“exogenous”)
Hence, what the estimates can teach us depends on what we cannot see This is a tricky situation: When can we trust our demand model? Answer 1: When we have exogenous price variation, hence corr(p,e)==0; OR Answer 2: When we observe all demand drivers; but this is difficult to verify
11a. Simulation
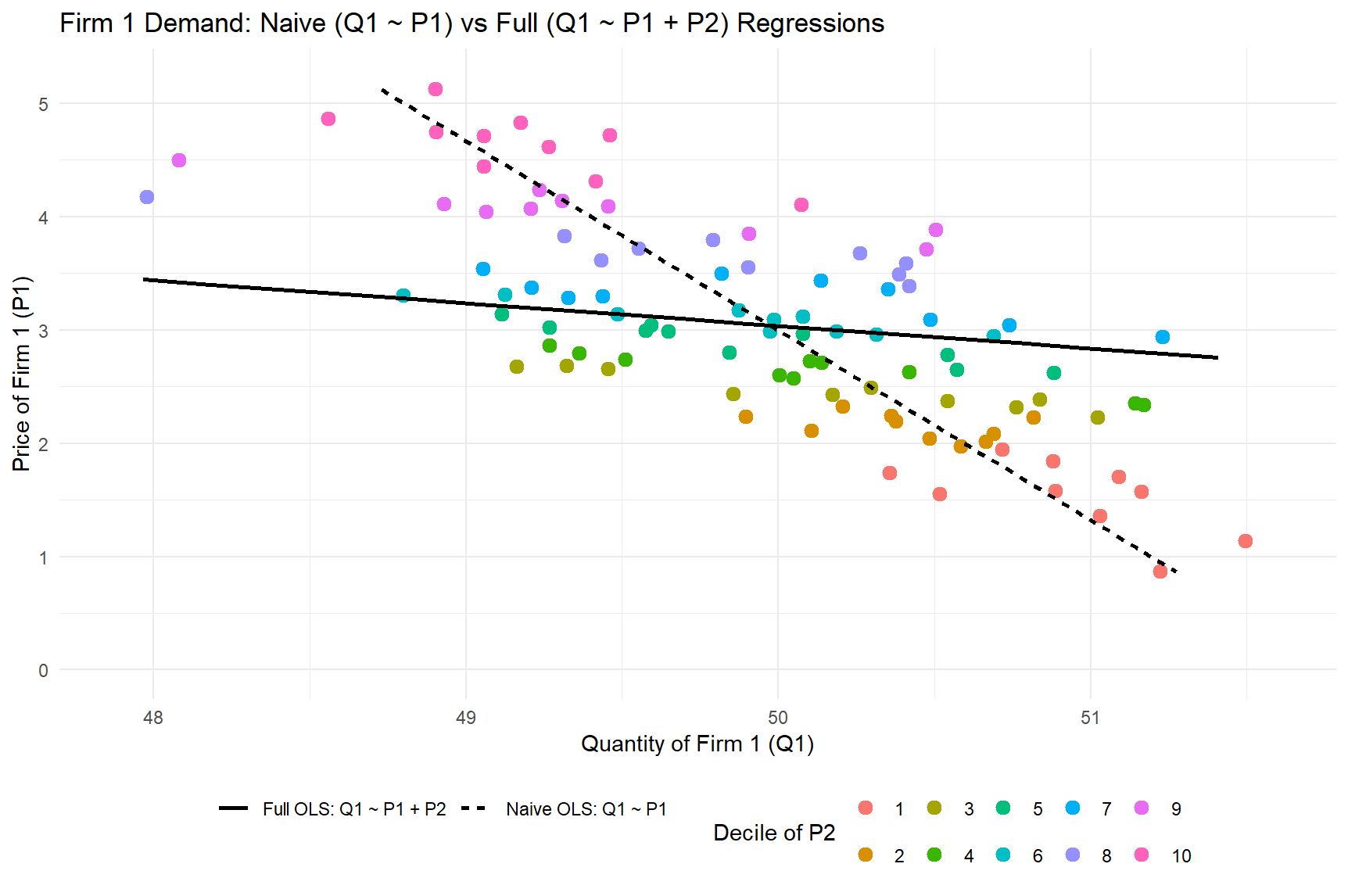
Suppose 2 firms, correlated cost shocks and correlated prices, MNL demand
Suppose true demand is \(q_1=f(p_1, p_2, \epsilon_1, \epsilon_2)\)
Suppose we use OLS to estimate \(q_1=\alpha + p_1\beta + \epsilon\)
We mistakenly believe that \(corr(p,\epsilon)==0\)
Incorrect: corr(p_1,p_2)>0, and p2 omitted, hence p2 is in epsilon\(\hat{\beta}\) is biased to fit the model’s assumption that \(\sum p_1\epsilon=0\)
Wrong \(\hat{\beta}\) means wrong demand curve slope
…implies wrong demand predictions in response to price
…recommended price will be wrong, may reduce profit
11b. Simulated data generating process
# 1. Simulation parameters and correlated cost shocks
set.seed(14) # for reproducibility
n_periods <- 100 # number of periods
market_size <- 100 # total market size (e.g. number of customers)
rho <- 0.9 # influence of costshock1 on costshock2
# Demand model parameters
alpha <- 0.2 # price sensitivity (common across products)
intercept1 <- 9 # baseline utility for product 1
intercept2 <- 9 # baseline utility for product 2
# (Outside option utility is normalized to 0)
# Simulate cost shocks for the two firms (correlated)
shock1 <- rnorm(n_periods)
shock2 <- rho * shock1 + (1 - rho) * rnorm(n_periods)
# Derive prices from costs (higher cost shock -> higher price)
base_cost <- 1
price1 <- 3 * base_cost + shock1
price2 <- 3 * base_cost + shock2
cor(price1, price2)
# 2. Compute market shares and quantities using multinomial logit demand
data <- tibble(
period = 1:n_periods,
shock1 = shock1,
shock2 = shock2,
price1 = price1,
price2 = price2
) %>%
mutate(
# Indirect utilities for each product and outside option:
U1 = intercept1 - alpha * price1,
U2 = intercept2 - alpha * price2,
U0 = 0, # outside option utility (baseline 0)
# Convert utilities to choice probabilities (logit formula):
expU1 = exp(U1),
expU2 = exp(U2),
expU0 = exp(U0),
share1 = expU1 / (expU1 + expU2 + expU0),
share2 = expU2 / (expU1 + expU2 + expU0),
Q1 = market_size * share1,
Q2 = market_size * share2,
Q0 = market_size * (1 - share1 - share2)
)
# Create decile variable for Firm 2's price
data <- data %>%
mutate(p2_decile = ntile(price2, 10))
# 3. OLS regressions for Firm 1's demand
model_naive <- lm(Q1 ~ price1, data = data)
summary(model_naive)
model_full <- lm(Q1 ~ price1 + price2, data = data)
summary(model_full)> # 3. OLS regressions for Firm 1's demand
> model_naive <- lm(Q1 ~ price1, data = data)
> summary(model_naive)
Call:
lm(formula = Q1 ~ price1, data = data)
Residuals:
Min 1Q Median 3Q Max
-1.31867 -0.34908 -0.00637 0.32919 1.19378
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 51.78942 0.17660 293.26 <2e-16 ***
price1 -0.59737 0.05565 -10.73 <2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.5011 on 98 degrees of freedom
Multiple R-squared: 0.5404, Adjusted R-squared: 0.5357
F-statistic: 115.2 on 1 and 98 DF, p-value: < 2.2e-16
> model_full <- lm(Q1 ~ price1 + price2, data = data)
> summary(model_full)
Call:
lm(formula = Q1 ~ price1 + price2, data = data)
Residuals:
Min 1Q Median 3Q Max
-4.177e-04 -6.103e-05 7.340e-06 7.187e-05 7.270e-04
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 5.000e+01 7.456e-05 670528 <2e-16 ***
price1 -4.999e+00 1.321e-04 -37832 <2e-16 ***
price2 4.998e+00 1.489e-04 33571 <2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.0001478 on 97 degrees of freedom
Multiple R-squared: 1, Adjusted R-squared: 1
F-statistic: 1.226e+09 on 2 and 97 DF, p-value: < 2.2e-16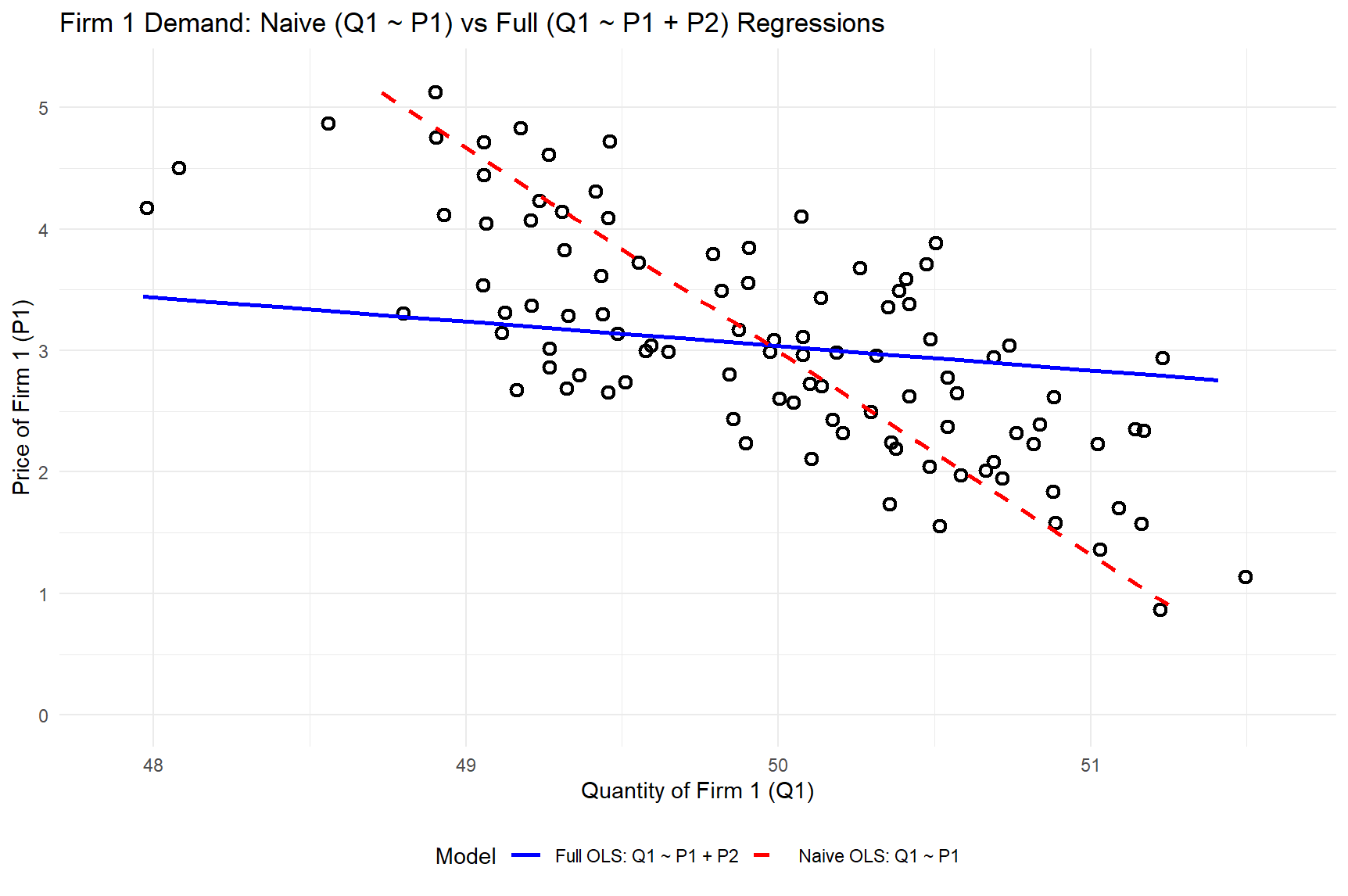
Common solutions
Experiments
Randomizing price eliminates confounding with unobservables Gold standard, but has drawbacks mentioned earlierQuasi-experiments using archival data
1. Instrumental variables 2. Regression discontinuities 3. Natural experiments 4. Difference-in-differences 5. Synthetic controls 6. Double/debiased machine learning These approaches are beyond the scope of this classModel the price-setting process
But without exogenous price variation, this is difficult to evaluateBest practice: Triangulate
Exogenous smartphone price variation
Smartphone discounts are randomly assigned,
thus we have exogenous price variation to identify \(\beta\)- This class focuses on how we can use demand models - Endogeneity remedies: Future metrics classes or graduate study - Treat the topic as a demand modeling risk to be understood

Describe price endogeneity in your own words
Generate a novel example related to price and demand Explain how to resolve it
Class script
- Wrangle data
- Estimate MNL
- Interpret parameters and SEs
- Assess model fit
Wrapping up
Recap
- Demand modeling enables data-driven sales predictions for counterfactual prices and attributes, facilitating profit maximization
- MNL is popular bc it is powerful, microfounded and tractable
- MNL has limitations (eg, IIA), but is extesnible by modeling heterogeneity
- Price endogeneity is a data problem that biases demand parameter estimates when price is correlated with unobserved supply or demand shifters. Usually resolved with exogenous price variation

Going further
